HANS WESTGEEST
 |
The Riddle Canon Solved |
|
Among the few surviving works of Ghiselin Danckerts are three riddle canons. Two extensive articles by P. J. de Bruijn devoted to the life of this Netherlandish composer (born in Tholen in the province of Zeeland) as well as to his compositions and his treatise on music theory,1 inform us that all three of these canons were printed in Naples. As Danckerts himself states in his treatise, the Ave maris stella was printed in 1535. Tua est potentia appeared in 1538. Although a precise date cannot be given for Ecce lignum Crucis, it seems likely that this canon, too, was first printed during the time that Danckerts was in the service of the Neapolitan nobleman Pierluigi Caraffa as an instrumentalist and composer. He held this position — exactly how long is not known — in the years prior to 1538, at which time he joined the papal chapel in Rome as a singer. Riddle canons undoubtedly owe their appeal not only to the musical qualities of the work concealed in them, but especially to the originality and ingenuity of the riddle itself. That the difficulty involved in finding the solution is in any case not the only criterion here is evident from Danckerts' canons. The fact that two of them went through several printings in the sixteenth century2 is already an indication that they were well liked by his contemporaries. We can infer that the composer himself was satisfied with his riddle canons from his later mention of all three of them when in his treatise3 he is defending the riddle canon against such depreciation as Nicola Vicentino had expressed in his L'antica musica ridotta alla moderna prattica (Rome, 1555).4 In terms of difficulty, however, these canons differ rather widely. Ecce lignum Crucis consists of a few lines of music which are printed in the form of a cross, together with a few inscriptions. The way in which the different voices of a six-part motet can be derived from this, and the way in which they have to be combined, was already set forth by Pietro Cerone in his voluminous work on music theory, El Melopeo y Maestro,5 which appeared in 1613. The solution to Tua est potentia is fairly simple.6 Five voices are printed in their entirety, while the six notes which together form the tenor can be found in the lilies of the accompanying illustration, the coat of arms of Pope Paul III. In both works the underlying idea is that one composition can be formed from various voices, one or more of which are cleverly concealed. A more complicated picture is presented by the best known of the three, Ave maris stella, which has the form of a chessboard and in which, as we shall see, a much larger number of motets has to be found. This piece is also discussed along with the many riddle canons and their solutions which take up the entire twenty-second book of Cerone's El Melopeo. In this chapter Danckerts' chessboard is the only 'enigma', however, which leaves Cerone himself expressing serious doubt about the solution he proposed. After him a few more attempts were made to formulate a solution,7 none of which can be considered satisfactory, however. After more than four and a half centuries the riddle has still not given up its secret.  Cerone assumes correctly that the motets to be found would always involve a combination of four voices. This is unambiguously indicated in the phrase 'Quatuor vocum unio' above the chessboard. Cautiously he puts forward the idea that the voices might have to be constituted by making movements across the board which correspond to the moves made by the pieces in a game of chess. 'Para dezir verdad, hasta agora no sè yo del cierto, como se haya de cantar: aunque voy pensando que las quatro partes que estan unidas en el tablero, vayan procedendo segun el juego del axedrez: y que este en alvedrio de los Cantores, el passar de una casilla à otra con aquel termino que mas agradare; advertiendo empero, que todas las quatro partes sean conformes en hazer el mesmo movimiento; de otra manera no saldrà bien el Canto.'The words, according to Cerone, expedite this process. In principle each voice always occupies a square of its own. Only on the diagonals of the board are there squares which can be touched by different voices at the same time. Due to the fact that some of the notes in them are full and others void, the melodies of the different parts in these squares are distinct. In the brief example which Cerone then gives, he lets two voices start in the Ave square at the upper left-hand corner and two in the square with the same word in the lower right-hand corner. All four voices move in different directions, first across three adjacent squares, with the result that all the voices produce a text consisting of the first three words of the Hymn to Mary, Ave maris stella; subsequently all four make a knight's move and land on a patris square. A great many motets can be formed in this way, although according to Cerone it cannot be assumed that this method will in all cases result in an acceptable motet. He concludes with the following words: 'Valga por lo que vale; y consideren que ha mas de ochenta años, que esta compuesto: y si no ay otro secreto mas deste, que dicho tengo, cada uno (a imitacion suya) podrà ordenar otro Canto, que sea mas fundado en las buenas reglas, y mas artizado.'Contradicting this cautiously proposed solution is the fact that the motto of the canon found above the chessboard plays no role in it whatsoever; there is, in fact, no relationship at all between the two. In addition it is certain that Danckerts, as we shall see, did not intend to offer with his chessboard a system for generating an indefinite number of motets. There are moreover considerations which prompt one to ask whether the proper approach is, after all, that of a 'chess-playing' reading. Danckerts' riddle canon Ave maris stella immediately calls to mind the chessboard poems of the French Burgundian rhétoriqueurs and of the rederijkers who practiced their art in the Low Countries. The idea behind these works is that the textual units found in the 64 squares have to be combined in such a way that they form poems. As to the manner in which this should be done, the reading methods to be applied, there has never been unanimity. Elsewhere8 I have reported on research which I undertook in order to throw some new light on the matter. This research, which was focussed primarily on the various 'arts de rhétorique' familiar to us from the rhétoriqueurs, involved the collecting of as many specimens and mentionings of the poetic form 'chessboard' (or 'échiquier') as possible. Taken individually, the chess¬boards yield little in the way of instructions about how they should be read. Only one specimen gives the reader somewhat more to go by: an example found in De Const van Rhetoriken (1555) by the Oudenaarde rederijker Matthijs de Castelein, who added to his chessboard the instruction that exactly 38 'baladen' (a kind of poem) should be found in it. Aided by various pieces of information gleaned from the material I had collected, I was able to arrive at what in my opinion is the correct solution. The 38 poems can in fact be found by performing a number, limited by inscriptions accompanying the chessboard, of systematic reading movements across the board, such as those following in either straight or zigzag fashion horizontal or vertical lines, or those following intersecting lines. What also became evident from this research is the fact that moving backwards was among the standard possibilities in reading the chessboard. Only one (atypical) example was found which has to be read in a different way.9 As far as the other chessboard poems are concerned, it is very likely necessary to think in terms of a comparable 'systematic' reading method. If Ghiselin Danckerts found the inspiration for his riddle canon in this poetic form, which, as it appears, was not infrequently used by his contemporaries — and the high degree of similarity hardly allows for doubt on this point — there is little reason to assume that he had a completely different type of solution in mind. A piece of information which was not available to Cerone and which is indispensible for solving the riddle can be found in Danckerts' own musical treatise, mentioned above, which was never published. At two places in this work it appears that the composer did indeed have a limited number of motets in mind as the solution. The quotations below I borrow from the articles by De Bruijn (italics mine). '... farò di nuovo stampare dopo tutti li concenti il detto concento composto da me in modo di schacchiero anchor'ch'io la facessi stampare un'altra volta molti anni addietro acciochè li musici ingegniosi, che si dilettano delle varie inventioni de canoni, ne facciano la notomia, et veggano se la possono far cantare in più di vinti differentiate maniere, ...'About these 'more than twenty ways' we are given more precise information in the second passage: 'Vicentino comanda ai compositori, che non debbiano far canoni sopra una torre, sopra un monte, sopra un flume, sopra lo schacchiero o sopra altre cose, sputando fuori molti suoi pareri goffi et vani, solamente per biasimare l'inventione del concento a quattro maniere, perciò che non solamente esso non ha saputo intendere l'inventione nemmeno il canto ma ni ancho ha saputo forse trovare per via delle sue regole una delle vinti maniere do poter la far cantare, et non havendo potuto li è restato nemico.'Evidently there is one motet to be found in the chessboard ('il canto') which is mentioned separately from the twenty other ways in which a vocal piece can be distilled from the board. With the term 'il canto' Danckerts is undoubtedly alluding to the motet Ave maris stella, which he previously in his text refers to as 'il motetto Ave Maris Stella a quattro voci nella forma di uno schacchiero'10 and which can be found in a fairly simple way. If attention is given to the words in the squares it soon becomes apparent that starting from the Ave squares at the upper left and lower right of the board, four voices can be assembled, each of which moves in a different direction across the entire chessboard, and which have as their text the same sequence of words. One of these moves from the upper left-hand corner through the horizontal rows to the corner on the lower right, a second begins at the lower right-hand corner and moves in the opposite direction to the upper left. Similarly, two parts can be found which move through the vertical columns and are each other's retrogrades.11 On the diagonals of the board each square contains both full notes and void notes, the one kind printed above the other. Either the full or the void notes have to be chosen for the different voices when they reach these squares. We can assume that the choice made the first time becomes binding for all subsequent occasions when the voices arrive at squares of this kind. The vertical parts always have to opt for the void notes. Due to the fact that in the two beginning squares these void notes are located closest to the notes which are respectively in the squares below and above, there is a natural tendency to make a vertical connection between them. At a number of other points where a choice between void and full notes has to be made for the vertical parts, the option of the void notes gives results which in melodic terms are by far the best.12 The full notes will always belong to the horizontal parts. To this ingeniously constructed motet, which ends in a clear cadence and here and there even includes a few groups of notes that imitate each other in various voices, as in some of the porta and dei squares, it seems impossible to add twenty more motets of 64 squares each. A further consideration is that retrograde reading, which, as already mentioned, is among the standard possibilities of the poetic form of the chessboard, also plays a role in Danckerts' composition. While looking for the other motets we have to keep this manner of reading in mind. And what are those twenty motets mentioned together as a group, separately from the great motet Ave maris stella, in the last quotation from Danckerts' treatise? Let us first take a closer look at the motto of the canon. Of this motto, 'Quod appositum est, et apponetur, per verbum dei benedicetur', the second half is the most transparent. In four squares, one on each side of the chessboard, we find the word 'dei', to which 'verbum dei' very possibly refers. Joining these words with each other produces a cross over the chessboard. Once this has become obvious, it seems fairly plausible to assume that the motets or voices covered by the cross are 'blessed' and thereby accepted, while others, for which this is not the case, will have to be eliminated. If this assumption is correct, it confirms our earlier conjecture that the twenty motets or the various voices constituting them all have to occupy fewer than 64 squares; they should, in fact, take up less than half of the chessboard. Otherwise they would all be covered by a cross. And to what does the first part of the motto, namely 'Quod appositum est, et apponetur' refer? In the motet Ave maris stella, which has been found and which in any case is one of the blessed solutions, the four combined voices are thoroughly intertwined in the chessboard. This suggests that 'appositum est' could refer to a combination of voices which takes place in a graphically comparable way. '(Quod) apponetur' can then refer to voices which are not interwoven in the chessboard in this way, but which can nevertheless be combined to form one composition. It is this interpretation of the motto that results in exactly twenty extra motets. Looking at the chessboard, one is immediately struck by the fact that its center is marked by two pairs of diagonally juxtaposed squares containing the same word. Each of the four squares belongs to different quarters of the board. Using the two iram squares as a starting point, we find in each of the two quarters to which these squares belong and which, as far as the text is concerned, are mirror images of each other, two parts. These four parts begin with the text iram vertas patris summi, and contain the word 'dei'. To arrive at this it is necessary to read horizontally through the four half rows or vertically through the four half columns until the alma squares at the lower left and upper right of the board are reached. In the same quarters of the chessboard three other motets can be similarly formed by beginning at the other's corners of the quarters. The motets to be found in this way are alma mater dei summi, which is the same as the one already mentioned except that it is in retrograde form, and summi dei mater alma and summi patris vertas iram, which are likewise each others opposites. It is unlikely that the twenty motets mentioned together as a group differ in length or that they have to be elicited from the chessboard in totally different ways. It therefore makes sense to determine whether more square shapes consisting of 16 small squares can be discovered, which, in a way similar to the four quarters of the board, contain groups of four voices that belong together and have the same text. There are indeed such square figures to be found, and as a result of the systematic arrangement of the words on the chessboard they form — as can be seen from Diagram 1 — a regular pattern. Diagram 1 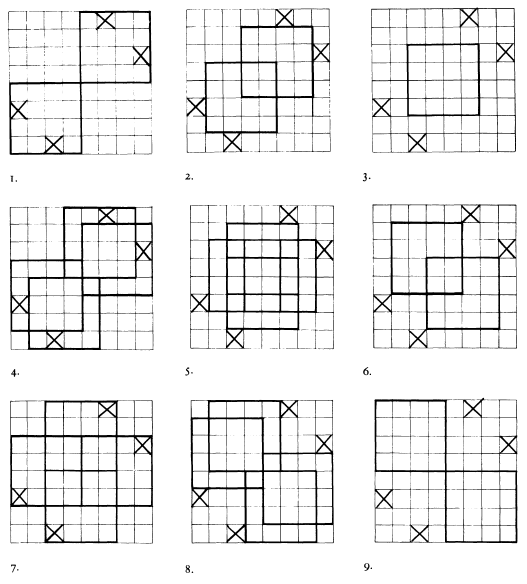 Only in figures 1, 4 and 7 of diagram 1 do all the square shapes, and thus all the voices, contain the word 'dei' (squares marked with a cross). In view of the canon motto the possibilities suggested by the other figures (2, 3, 5, 6, 8 and 9) have to be eliminated. As we have seen, four four-part motets can be distilled from two quarters (see figs. 1-4 in diagram 2). In the square shapes of figures 4 and 7, different series of words result from readings in two directions starting from each corner (see figs. 5-12 en 13-20 in diagram 2). These words form the text of two parts of different motets. Exactly twenty motets can be found in this way. In Diagram 2 only the beginning of the four voices of these motets is indicated with an arrow. The rest of the small squares within the large square figures have to be added along lines running parallel to the arrows. Thus the four voices in figure 1, for example, form the motet in Example 2. Diagram 2 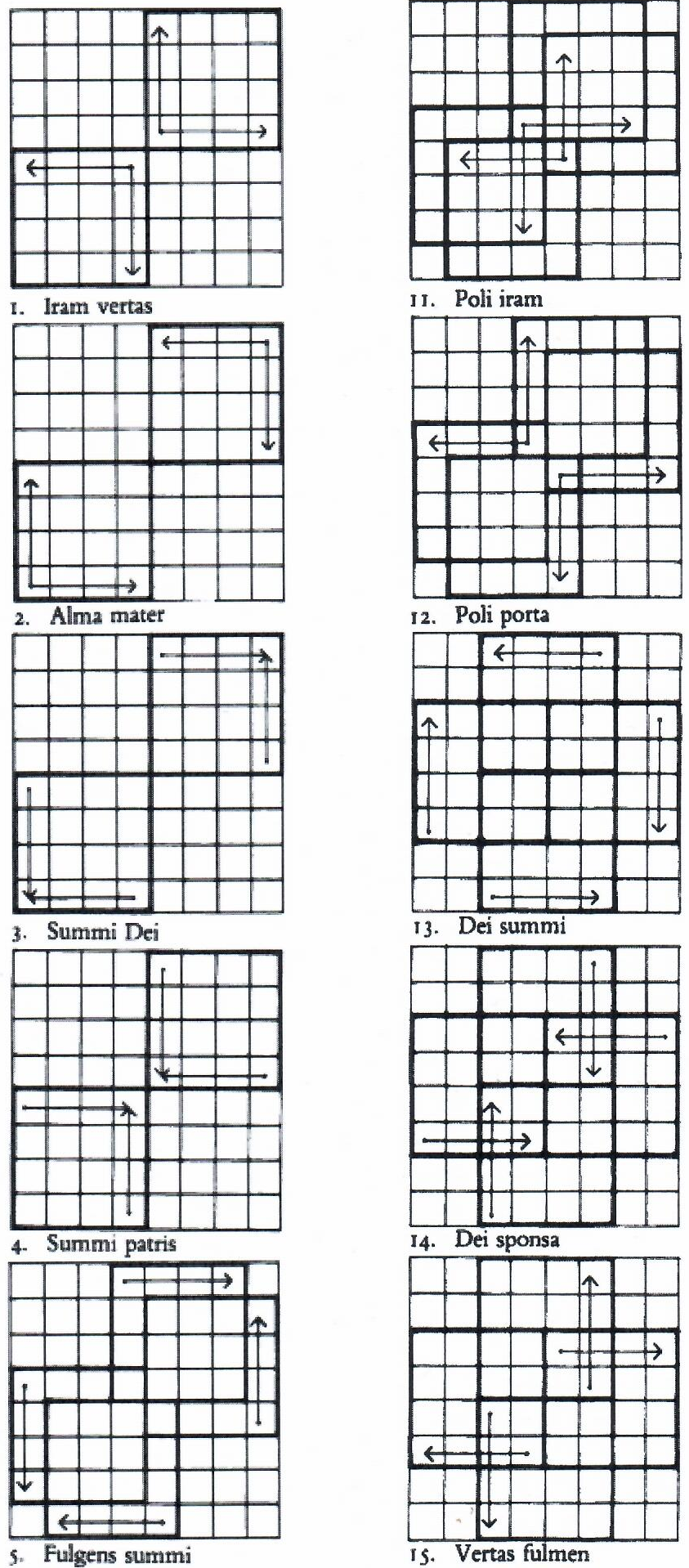 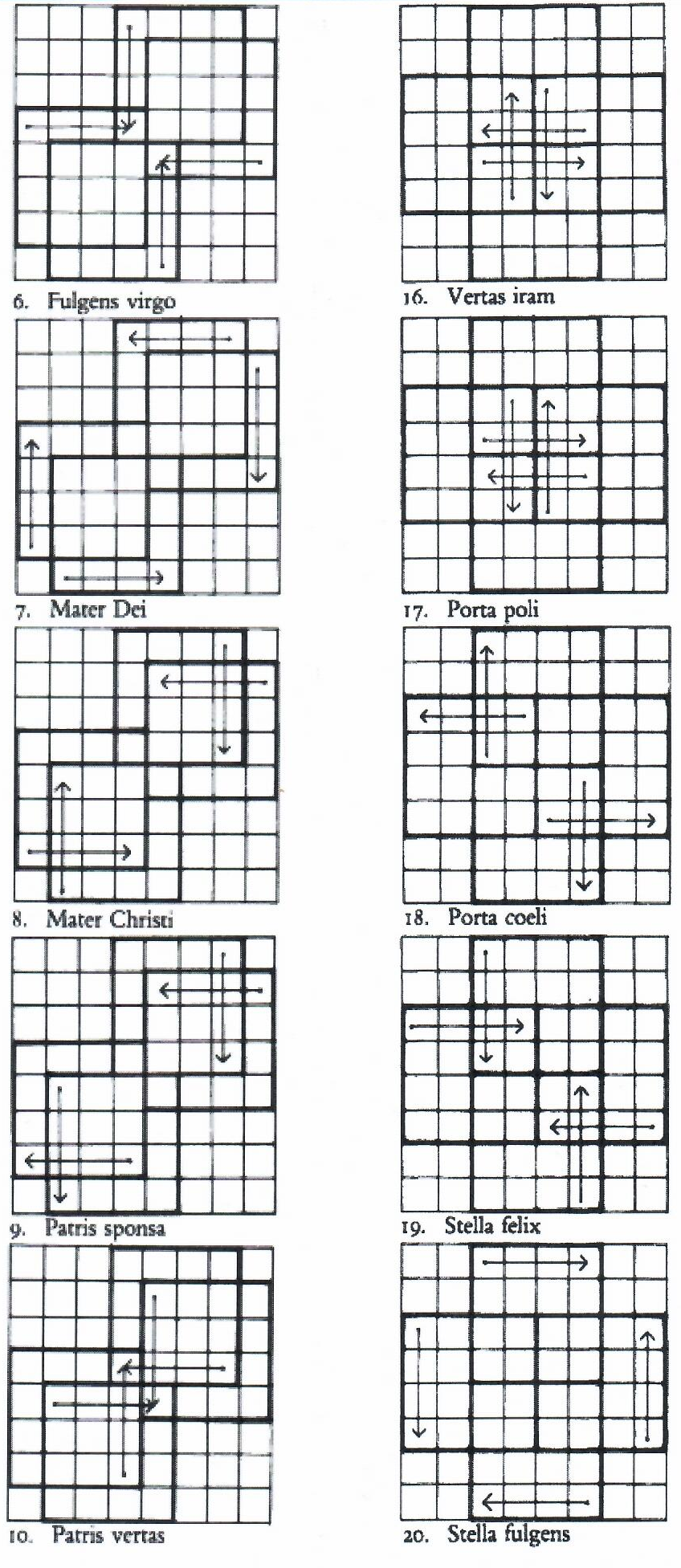 With his Ave maris stella Ghiselin Danckerts left us, in a form familiar to him from the poetry of his time, a riddle canon which has proved to be as ingenious as it is difficult to solve. For his contemporaries, who were at home with the literature of the age and were familiar with the reading techniques commonly applied to poems of this kind, the solution probably suggested itself more readily, although for them, too, it must have presented its share of problems. The knowledge that Danckerts' riddle has to be read by means of systematic movements which can also be carried out in retrograde fashion is indispensable to the solution of this riddle. We, centuries later, have only been able to determine this thanks to our move onto a different square of the scholarly chessboard, and to the blessing under which this move seemed to rest. Example 1  Example 2   1) P. J. de Bruyn, ‘Ghisilinus Danckerts, kapelaan-zanger van de Pauselijke kapel van 1538 tot 1565 — Zijn leven, werken en onuitgegeven tractaat’, in Tijdschrift der Vereeniging voor Noord-Nederlands[e] Muziekgeschiedenis 16 (1946), pp. 217-252, and 17 (1955), pp. 128-157. About the canons see especially TVNM 16, p. 225, and 17, pp. 129-133.
2) Ave maris stella was reprinted on a single sheet by Melchior Kriesstein in Augsburg in 1549 (Répertoire International des Sources Musicales, A I, 2, D 888). Tua est potentia was also included in the collection published by this printer in 1540, Selectissimae necnon familiarissimae cantiones (RISM, B I, I, 15407), as well as in Concentus octo, sex, quinque & quatuor vocum published in 1545 by Philipp Ulhard, also in Augsburg (RISM, B I, 1, 15452). 3) About this treatise which was never published, and of which Danckerts wrote three different versions between 1551 and 1560, see De Bruyn 1955, pp. 147-157. 4) See N. Vicentino, L'antica musica ridotta alla moderna prattica. (Rome, 1555; Faks.-Nachdr. hrsg. von E. Lowinsky, Kassel enz., 1959. Documenta Musicologica I, 17), fol. 93r-v. 5) P. Cerone, El melopeo y maestro : tractado de musica theorica y pratica. (Naples, 1613; facs.-ed. Bologna, 1969, Bibliotheca Musica Bononiensis II, 25. 6) See De Bruijn 1955, pp. 131-133. 7) See A. Auda, La Musique et les Musiciens de l'Ancien Pays de Liège. (Liège, 1930), p. 277, and S. Stribos, ‘De raadselcanons uit de 15e en 16e eeuw’, deel 7, in Huismuziek 5 (1985), pp. 7-9. See also note 11. 8) See my article ‘Casteleins code gekraakt’ in De Nieuwe Taalgids 80 (1987), pp. 111-124. 9) The chessboard poem referred to here is found in Les Controverses des sexes masculin et fémenin (Toulouse, 1534) by Gratien Du Pont. An explanatory note by the author makes it clear that he was aware of the atypical nature of his (ideas about the) chessboard; see the article mentioned in note 8. 10) See De Bruijn 1955, p. 130. 11) The solution proposed by Auda (see note 7) coincides with the first fragment of the motet indicated here. The four voices are formed by only the first eight of the 64 squares. See Example 1, up to and including the word Alma. (Two small deviations are the result of mistakes made in the transcription, another is due to a different interpretation of the chessboard from Cerone's El melopeo in the representation used by Auda.) Nor did Stribos get further than a proposal for one of the required solutions. He combined the same four parts as Auda (but following Kriesstein's edition), leaving out, however, the squares fulgens summi. The very small motet which results from this has as its text the first six words of the original hymn Ave maris stella. 12) See for the part beginning at the upper left the sequence of the melody fragments found together with sponsa-christi, sponsa-fulmen and maris-ave, and for the vertical part those with mater-alma and vertas-fulmen.
|